La numération D'ni
De Mystpedia.
m |
m |
||
| Ligne 1 : | Ligne 1 : | ||
<!-- ************************************************** --> | <!-- ************************************************** --> | ||
| - | = | + | = Les chiffres D'ni= |
| Ligne 31 : | Ligne 31 : | ||
(On remarquera que tous les nombres sont représentés dans des boîtes aux côtés horizontaux à peine plus longs que les verticaux) | (On remarquera que tous les nombres sont représentés dans des boîtes aux côtés horizontaux à peine plus longs que les verticaux) | ||
| - | == | + | ==Les 4 chiffres de base== |
Tous les autres nombres sont basés sur quatre symboles différents : | Tous les autres nombres sont basés sur quatre symboles différents : | ||
| Ligne 44 : | Ligne 44 : | ||
[[Image:1111.jpg|center|moulage]] | [[Image:1111.jpg|center|moulage]] | ||
| - | =="puissances de 5"== | + | ==Les "puissances de 5"== |
Aussi, ces quatre symboles peuvent être tournés 90 degrés dans le sens inverse des aiguilles d'une montre pour représenter les diverses Â⫠puissances de cinq Â⻠: | Aussi, ces quatre symboles peuvent être tournés 90 degrés dans le sens inverse des aiguilles d'une montre pour représenter les diverses Â⫠puissances de cinq Â⻠: | ||
| Ligne 57 : | Ligne 57 : | ||
5, 10, 15, 20 s'appellent respectivement : '''[[Vaht|vaht]], nayvoo, heebor, rish'''. | 5, 10, 15, 20 s'appellent respectivement : '''[[Vaht|vaht]], nayvoo, heebor, rish'''. | ||
| - | == | + | ==Construction des nombres== |
Ensuite, prenons par exemple le nombre 19 qui se traduit en anglais par (nineteen, et plus loin, nine-ten) ; les D'ni ont la même construction de nombreâ€⦠| Ensuite, prenons par exemple le nombre 19 qui se traduit en anglais par (nineteen, et plus loin, nine-ten) ; les D'ni ont la même construction de nombreâ€⦠| ||
Version du 31 mars 2010 à 20:54
Sommaire |
Les chiffres D'ni
Généralités
Le système de numération de D'ni, à la différence de presque tout les systèmes de la terre, utilise la base-25 plutôt que la base-10. En effet nous employons la base-10 parce que nous avons 10 doigts sur nos mains...alors que le D'ni a semblé employer la même rationalisation, mais au lieu d'ajouter des doigts de la gauche vers la droite, il les a multipliés (5*5 = 25). C'est un système très efficace. En outre, l'alphabet D'ni et les nombres proviennent du même système.
Par exemple dans le Grec, les lettres et les nombres ont été employés l'un pour l'autre:
En D'ni c'est à peu près la même chose sauf que les symboles sont représentés dans des boîtesâ€â¦
Par la suite, alors que les nombres demeuraient plus ou moins réels, les lettres sont devenues plus cursives dans l'aspect :
Savoir ainsi vos nombres est l'une des meilleures manières de pouvoir identifier des lettres.
Il y a 25 nombres, s'étendant de 0 à 24.
Zéro (roon) peut être vu partout ; dans le grand zéro, dans votre étagère de Relto, et dans votre KI. Il ressemble à une boîte avec un point.
(On remarquera que tous les nombres sont représentés dans des boîtes aux côtés horizontaux à peine plus longs que les verticaux)
Les 4 chiffres de base
Tous les autres nombres sont basés sur quatre symboles différents :
Ils représentent respectivement 1, 2, 3 et 4, en D'ni : Fah, Bree, Sen, Tor.
Pour s'en rappeler on voit la ressemblance dans les chiffres :
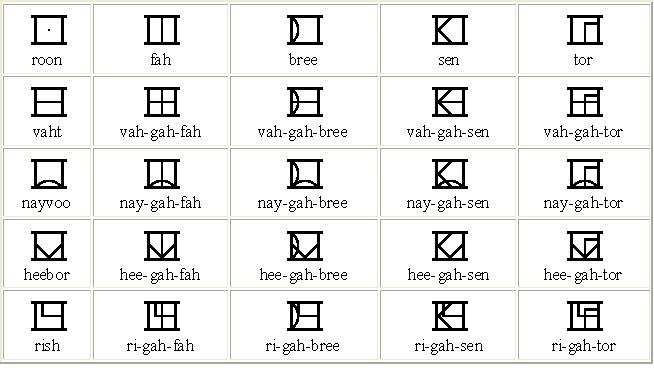
Les "puissances de 5"
Aussi, ces quatre symboles peuvent être tournés 90 degrés dans le sens inverse des aiguilles d'une montre pour représenter les diverses Â⫠puissances de cinq Â⻠:
Donc 1 tourné en longueur = 5 ; 2 en longueur = ( 5*2) 10
3 tourné en longueur= 15, 4= 20,
5, 10, 15, 20 s'appellent respectivement : vaht, nayvoo, heebor, rish.
Construction des nombres
Ensuite, prenons par exemple le nombre 19 qui se traduit en anglais par (nineteen, et plus loin, nine-ten) ; les D'ni ont la même construction de nombreâ€â¦
Par exemple : 14, est l'assemblage du symbole 10 et du symbole 4â€⦠(10+4 = 14)
Dans le langage parlé on utilisera des contractions des racines Ainsi vaht (5) nayvoo (10) heebor (15) et rish (20) ; se transformeront dans la langue en : Vah, nay, hee et riâ€⦠puis on y ajoute le mot Â⫠et Â⻠= gah. Enfin le dernier chiffreâ€â¦
Par exemple, 14 se dit NAY-GAH-TOR, (on a bien Ââ«10 ET 4 Ââ»)
Par conséquent, nous obtenons ce qui suit :
on a en 1ere ligne: 0 1 2 3 4 on a en 1ere colonne: 0 5 10 15 20
On remarquera que l'addition d'une ligne et d'une colonne se trouve à son intersectionâ€â¦
(Par exemple : vaht (5) plus bree (2) = vah-gah-bree (7))
Il est possible qu'en comptant sur leurs mains, les D'ni aient tourné une main pour représenter les Â⫠puissances de cinq Ââ», c'est pourquoi elles sont écrites comme étant décalés d'un quart de tour. (Les boite représentant les nombres)
Nous, ayant un système base 10, chaque chiffre se trouvant à gauche représente une puissance additionnelle de 10â€â¦
Par exemple le nombre 9573 = 3 + (7*10) + (5*10*10) + (9*10*10*10)
De la même manière en D'ni quand on Â⫠décale à gauche Â⻠on multiplie par 25 â€â¦
D'où 9573(de chez nous)= 3 + ( 7*25) + ( 5 * 25*25) + ( 9*25*25*25)= 143 928
Numérations des différentes grandeurs
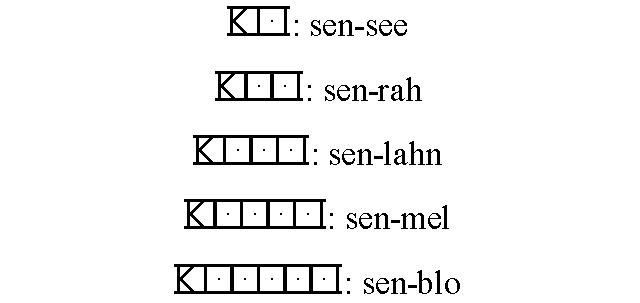
Enfin, pour étudier les grandeurs (centaines, milliersâ€â¦) on prendra l'exemple du chiffre 3 (sen). Il suffit de prendre la base (ici SEN, 3) et d'y ajouter un suffixe on a see pour les dizaines ; rah pour les centaines â€â¦..
On a donc en commençant par les dizaines :
On peux écrire 11 par exemple: fah-see-fah
Remarques
Félicitations vous pouvez désormais compter jusqu'à 25 millionsâ€â¦
En notant par ailleurs que chez les D'ni, le chiffre 25 à toujours été très important, 25 grands héros célébrés dans la salle, employé sur des horloges et les cadrans afin de représenter le numéro zéro et le numéro 25. Vous pouvez le voir sur l'horloge de Gehn dans Riven, aussi bien que certains des afficheurs de défilement dans le grand zéro.